Pure Data e i modelli audio

Disclaimer: Il contenuto di questo post è un estratto della mia tesi di laurea, realizzata nel 2006. Alcuni esempi potrebbero risultare obsoleti, tuttavia la componente teorica resta un buon riferimento per chi deve approcciarsi alla materia.

Il modello di rotolamento

Tra le comuni interazioni meccaniche che coinvolgono oggetti solidi, il rotolamento forma una categoria interessante anche dal punto di vista dell’audio: l’esperienza di tutti i giorni ci dice che il suono prodotto da un oggetto rotolante viene spesso riconosciuto come tale, e in generale è distinto da altri suoni come quelli dovuti allo sfregamento anche degli stessi oggetti. Ciò potrebbe essere dovuto alla natura del rotolamento come un processo di interazione continua, dove la forza mutua sugli oggetti coinvolti è descritta come un impatto senza l’aggiunta di forze di frizione perpendicolari. Oltre ad essere caratteristici, i suoni di rotolamento portano importanti informazioni: in aggiunta alle caratteristiche di risonanza degli oggetti coinvolti (che dipendono da forma, dimensione e materiale), altri attributi vengono espressi nel suono, attributi di trasformazione, come velocità, gravità o accelerazione/decelerazione. Lo sviluppo di un modello di rotolamento espressivo e in tempo reale da presupposti fisici, acustici e implementativi è descritto di seguito.

L’interazione di rotolamento con il modello di impatto come blocco di base

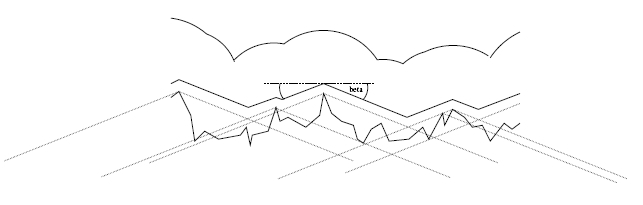
Contrariamente ad azioni quali lo sfregare o il grattare, la forza di interazione dei due oggetti coinvolta in un semplice scenario di rotolamento (l’oggetto rotolante e il piano) è perpendicolare alla superficie di contatto (la curva media macroscopica), diretta lungo la linea che connette il punto di contatto e il centro di gravità dell’oggetto rotolante. Le condizioni di contatto devono essere modificate per riflettere le varie distanze della superficie di contatto. L’oggetto rotolante è assunto come localmente sferico, senza dettagli macroscopici sulla superficie. E’ possibile fare queste assunzioni dal momento che i dettagli microscopici della superficie dell’oggetto rotolante possono essere semplicemente aggiunti alla superficie sulla quale l’oggetto rotola, e può essere variato il raggio di curvatura della superficie stessa; vedremo che anche l’assumere un raggio costante può essere soddisfacente per la maggior parte degli scopi. E’ importante notare che il contatto tra i due oggetti durante il rotolamento è ristretto a punti distinti: il piano non viene seguito nella sua interezza.

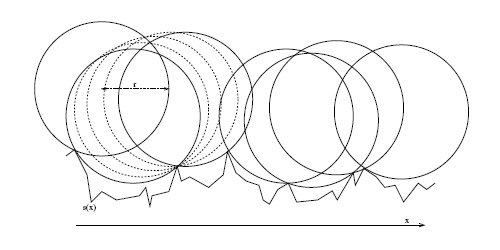
Il movimento reale dell’oggetto rotolante si differenzia da questa idealizzazione a causa dell’elasticità e dell’inerzia. In buona approssimazione, il movimento verticale del centro della palla è calcolato con un modello di impatto unidimensionale con la curva in figura 1. I punti di contatto e la traiettoria risultante, che idealmente dovrebbe essere applicata al modello di impatto unidimensionale, sono rappresentati in figura 2. Il calcolo esatto dei punti di contatto è dispendioso in termini di risorse computazionali: in ogni punto \(x\) lungo la curva della superficie, cioè per ogni punto di campionamento nel caso discreto (dove la frequenza del campionamento è la stessa del campionamento audio), deve essere calcolata la seguente funzione che descrive l’attuale punto \(p_x\) :

dove

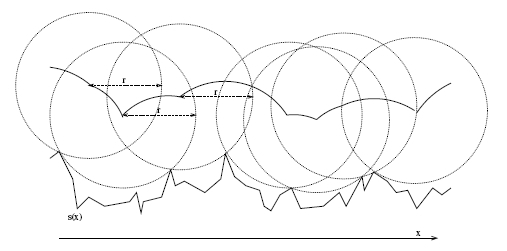
La curva ideale viene poi calcolata da questi punti di contatto. Una tecnica più semplice (e quindi anche meno dispendiosa in termini di risorse di calcolo) è rappresentata in figura 3. La traiettoria in figura 2 converge alla curva ideale di figura 3 per raggi molto grandi se comparati alla ruvidità della superficie. Infatti, in una prima implementazione, anche le forti semplificazioni (riportate figura 4 realizzate con un algoritmo molto semplice, hanno dato risultati convincenti.

La superficie

Esistono diverse tecniche per realizzare il profilo della superficie alla base del modello di rotolamento. Una possibilità è quella di campionare o effettuare una scansione di superfici reali e usare tali segnali come input per lo stadio seguente del modello; questo approccio però non si adatta ai nostri obiettivi: noi siamo interessati ad un modello parametrico, flessibile ed efficiente piuttosto che ad una singola simulazione realistica. Inoltre i segnali memorizzati sono difficili da adattare alle variazioni degli attributi del modello; preferiamo quindi usare modelli statistici di superfici che possano efficientemente generare segnali per i vari attributi.

E’ comune nella computer graphics descrivere le superfici tramite metodi frattali. L’applicazione di questa idea al nostro modello unidimensionale conduce all’utilizzo di un segnale di rumore con spettro di potenza \(1/f^{\beta}\), o equivalentemente rumore bianco filtrato con queste caratteristiche. Il parametro reale \(\beta\) riflette la dimensione frattale (o ruvidità). I risultati pratici di questo tipo di modello sono diventati più convincenti quando la banda del segnale della superficie è stata fortemente limitata; ciò non deve sorprendere se pensiamo che solitamente le superfici coinvolte nel rotolamento sono molto smussate. Smussare su larga scala (che può essere assimilato al tagliare pezzi di pietra per pavimentazioni) corrisponde ad un filtraggio passa–alto, mentre smussare a livello microscopico (come lucidare una pietra) può essere visto come un filtraggio di tipo passa–basso. Tramite queste elaborazioni però si possono perdere le caratteristiche del rumore \(1/f^{\beta}\) di partenza. Perciò optiamo per una approssimazione di questa curva con un filtro del secondo ordine la cui ripidità è proporzionale al grado di ruvidità a livello microscopico.

Tutte le frequenze in questo modello di basso livello devono variare proporzionalmente ai parametri di velocità, perciò l’ampiezza del segnale di superficie deve essere mantenuta costante. Naturalmente i parametri dell’impatto, in particolare la costante di elasticità \(k\), devono essere variati opportunamente a seconda della superficie che si vuole simulare (cioè in base alle proprietà del materiale), in quanto contribuiscono fortemente alla espressività del modello.

Il modello di impatto

Un suono di contatto è descritto tramite due sistemi, uno per l’oggetto risonante e uno per l’oggetto percussore. Supposto che la superficie di contatto sia piccola, la forza di contatto viene espressa come:

dove \(v(t) = \dot{x}(t)\) è la velocità di compressione, \(k\) è il coefficiente di rigidità, \(\alpha\) è un parametro che descrive la geometria locale dell’impatto (nel caso di due perfette sfere vale 1.5), \(\lambda\) è un coefficiente di smorzamento e \(\mu = \lambda/k\) è un termine matematico (senza significato fisico) detto caratteristica viscoelastica.

Il percussore è considerato una massa ideale, quindi l’unico parametro che lo caratterizza è la massa; il risonatore invece è un oggetto modale ed è caratterizzato dai parametri di frequenza, tempi di decadimento, \(k\), \(\alpha\) e \(\lambda\). Si assume inoltre che il percussore abbia un elevato coefficiente di smorzamento: in tal modo diventa trascurabile l’energia acustica delle sue vibrazioni, e l’energia viene trasferita al risonatore che emette il suono. Per una descrizione matematica vengono sintetizzati i modi di vibrazione (teoricamente infiniti), ognuno dei quali fornisce un contributo allo spettro del segnale (Avanzini, F., Rath, M., & Rocchesso, D., 2003).

Caratteristiche di alto livello

Oltre ai parametri di basso livello visti nella sezione precedente, i tipici moti di rotolamento posseggono caratteristiche a livello macroscopico che contribuiscono fortemente alla percezione acustica, e non possono essere descritti come fatto in precedenza. Molte superfici contengono dei pattern più o meno regolari che non possono essere classificati come rumore frattale filtrato, e tali periodicità possono essere verificate attraverso l’esperienza di tutti i giorni: i pavimenti in pietra, o i solchi pseudoperiodici in molte tavole di legno. Le singole irregolarità sulla superficie dell’oggetto rotolante possono essere raggruppate in una sola categoria, dal momento che sono richiamate periodicamente nel movimento rotatorio. Tale caratteristica può essere modellata con segnali impulsivi di frequenza costante o variante in un piccolo intervallo; potrebbero essere utili delle approssimazioni sinusoidali o polinomiali, con un parametro di smussamento legato al grado di approssimazione della funzione. Ancora, le frequenze devono variare proporzionalmente alla velocità.

Dev’essere fatta un’altra osservazione a livello macroscopico: per oggetti rotolanti che non sono perfettamente sferici (in maniera rilevante per il movimento) la velocità del punto di contatto su entrambe le superfici e l’effettiva forza che preme l’oggetto rotolante sulla superficie variano periodicamente; devono essere variati questi due parametri per modellare tale deviazione dalla sfericità perfetta.

Infine notiamo che, come nell’ascolto di tutti i giorni, gli scenari acustici del rotolamento di oggetti sono riconosciuti e accettati più facilmente se sono presenti dinamiche tipiche; ad esempio pensiamo al suono di una palla che cade e che rimbalza fino a quando non raggiunge un contatto costante con il suolo: a questo punto il rotolamento diventa chiaro dal punto di vista uditivo e la velocità media lentamente diminuisce fino diventare nulla.

Tessiture della superficie

Molti dei suoni di contatto ai quali siamo interessati non possono essere ricreati in modo convincente usando solo modelli deterministici, come nel caso dei suoni di rotolamento risultanti dalla sequenza di micro impatti tra due oggetti risonanti, determinati dal profilo della superficie di contatto. Affrontiamo quindi il problema di effettuare il rendering delle tessiture di superfici attraverso processi frattali; tali processi sono molto usati nella computer graphics, dal momento che forniscono tessiture che sembrano naturali all’occhio umano. Dato che nei modelli fisici le proprietà delle superfici vengono tradotte direttamente in segnali di forza e, di conseguenza, in suoni, sembra naturale seguire lo stesso approccio per modellare le superfici.

I frattali sono definiti (Hastings, H. M. & Sugihara, G., 1993) come geometrie invarianti rispetto alla scalatura. Sono auto–simili se la scalatura è isotropica o uniforme in tutte le direzioni, auto–affini se la scalatura è anisotropica o dipendente dalla direzione, staticamente auto–simili se sono l’unione di copie di se stessi scalate statisticamente. Più formalmente, un processo frattale unidimensionale può essere definito come una generalizzazione della definizione di moto standard Browniano (Resnick, S., 1992).

Il processo stocastico \(x = \{x(t),t \geq 0\}\) è un moto standard Browniano se:

1. il processo stocastico \(x\) ha incrementi indipendenti;
2. vale la proprietà \(x(t) - x(s) \sim N(0,t-s) \hspace{0,5cm} per \hspace{0,5cm} 0 \leq s < t;\) cioè l’incremento \(x(t) - x(s)\) è normalmente distribuito con media nulla e varianza \((t-s)\);
3. è vero che \(x(0) = 0.\)

La definizione di moto standard Browniano può essere generalizzata alla definizione di processo frattale se l’incremento \(x(t)-x(s)\) è normalmente distribuito con media 0 e varianza proporzionale a \((t-s)^{2H}\). Il parametro H è chiamato esponente di Hurst e caratterizza il comportamento del processo frattale rispetto alla scalatura: se \(x=\{x(t),t \geq 0\}\) è un processo frattale con esponente di Hurst \(H\), allora, per ogni reale \(a > 0\), obbedisce alla seguente relazione di scala:

dove \(\stackrel{P}{=}\) denota l’uguaglianza statistica. Questa è la definizione formale di auto–similirarità statistica. La famiglia di processi \(1/f\) statisticamente auto–simili, nota anche come rumore \(1/f\), è composta da processi aventi densità di spettro di potenza \(S_x(\omega)\) proporzionale a \(1/ \omega^{\beta}\), con \(\beta\) legato all’esponente di Hurst \(H\) dalla relazione \(\beta = 2H + 1\). Per \(\beta = 0\) la definizione corrisponde al rumore bianco, per \(\beta = 2\) si ottiene il rumore Browniano, e per \(\beta = 1\) il rumore risultante è rumore rosa. Il parametro \(\beta\) è in relazione anche con la dimensione frattale. La dimensione frattale (Wornell, G. W., 1998) di una funzione è un parametro reale che determina l’irregolarità di un oggetto frattale, è legata al grafico della funzione ed è usata nella computer graphics per controllare la ruvidità percepita (Pentland, A. P., 1988). Per i processi \(1/f\), tale dimensione è inversamente proporzionale all’esponente di Hurst \(H\): valori maggiori di \(H\) corrispondono a valori minori della dimensione frattale; \(H\) è proporzionale a \(\beta\). Perciò, incrementando \(\beta\) possiamo raggiungere una redistribuzione della potenza dalle alte alle basse frequenze, con uno smussamento complessivo della forma d’onda.

Il problema di generare il rumore \(1/f\) è stato trattato estensivamente. Uno degli approcci più comuni risulta quello di filtrare una sorgente di rumore bianco per ottenere lo spettro \(1/f\); seguendo questo procedimento utilizzeremo il modello riportato in (Saletti, R., Novembre 1986) e (Corsini, G. & Saletti, R., Dicembre 1988). Il filtro è una cascata di N filtri del primo ordine, ognuno con una coppia di poli e zeri; la funzione di trasferimento \(H(s)\) nel dominio di Laplace è la seguente:

dove \(A\) è una costante. Il generatore di rumore frattale è ottenuto impostando opportunamente i poli e gli zeri dei filtri nella cascata (Saletti, R., Novembre 1986). In particolare, il polo e lo zero alle frequenze \(f_{pi}\) e \(f_{0i}\) possono essere computati come funzioni di \(\beta\) con le seguenti formule:

dove \(f_{p1}\) è il polo di frequenza più bassa del filtro; perciò il limite inferiore della banda di frequenza per l’approssimazione è \(f_{p1}\). La densità \(h\) (densità dei poli per decade di frequenze) può essere usata per controllare l’errore tra lo spettro desiderato e lo spettro approssimato ottenuto dal filtraggio del rumore bianco. La dipendenza dell’errore in relazione alla densità dei poli del filtro è discussa in (Corsini, G. & Saletti, R., Dicembre 1988). La figura mostra uno spettro \(1/f^{\beta}\) ottenuto usando il filtro \(f_{pi}\), con due diversi valori per \(h\).

La funzione di trasferimento nel dominio discreto del tempo può essere computata con il metodo della varianza della risposta all’impulso (Mitra, S. K., 1998); ciò corrisponde a mappare poli e zeri della funzione di trasferimento \(H(s)\) su poli e zeri della funzione di trasferimento \(H(z)\) nel dominio discreto del tempo attraverso la seguente sostituzione:

dove \(T_s\) è il periodo di campionamento e \(s_x\) indica un polo \(s_{pi}\) o uno zero \(s_{0i}\). Si ottiene la seguente funzione di trasferimento discreta:

dove \(A'\) è una costante di normalizzazione. In conclusione, lo spettro \(1/f^{\beta}\) è approssimato da una cascata di filtri del primo ordine, ognuno con la seguente funzione di trasferimento discreta:

Implementazioni dei modelli in Pure Data

Cos’è Pure Data

Pure Data è un software ideato da Miller Puckette: si tratta di un ambiente di programmazione visuale in real–time per l’elaborazione di audio e grafica, basato sul sistema Max/MSP ma più semplice e portabile di questo. Sono presenti due caratteristiche in PD molto importanti: la possibilità di gestire contemporaneamente la simulazione video e la simulazione audio utilizzando il pacchetto GEM di Mark Dank e delle facilitazioni nelle definizioni nell’accesso alle strutture dati.

Ogni documento di PD è chiamato patch; una volta che tale file viene aperto si presenta composto di una finestra principale e di eventuali sotto–finestre (che possono essere visualizzate o nascoste ma sono sempre in esecuzione). In ogni finestra compaiono dei blocchi collegati tra loro; i blocchi possono essere di quattro tipi:

Oggetti

Un oggetto viene creato scrivendo del testo all’interno del blocco; il testo viene diviso in atomi: il primo atomo definisce il tipo di oggetto che viene creato, i successivi costituiscono gli argomenti di creazione, i quali servono ad inizializzare l’oggetto.

Ogni oggetto può possedere zero o più inlet (collegamenti in input) e zero o più outlet (collegamenti in output); il numero di questi dipende dal tipo di oggetto. Ci sono due tipi di collegamento: collegamenti di segnale e collegamenti di controllo; i primi sono rappresentati da una linea marcata, mentre i secondi da una linea sottile. La scelta del tipo di collegamento dipende dall’outlet dal quale provengono; un outlet può essere collegato ad un inlet solo se entrambi accettano collegamenti dello stesso tipo (o entrambi di segnale o entrambi di controllo).

In figura è riportato un esempio di oggetto: l’atomo 1+1 definisce la tipologia di oggetto (un blocco sommatore), mentre il secondo atomo 13 indica il valore da sommare all’ingresso.

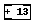
Messaggi

I blocchi di messaggio interpretano il testo come un messaggio da inviare ogni volta che il blocco viene attivato; l’invio è verso il blocco al quale l’outlet è collegato e può avvenire un numero qualsiasi di volte durante l’esecuzione della patch. Il blocco di messaggio possiede sempre un inlet e un outlet. Nell’esempio seguente il primo blocco, quando viene attivato dal click del mouse, invia il messaggio 21 all’oggetto che lo sommerà a 13 all’ultimo blocco viene inviato il risultato dell’operazione.

Un messaggio può essere attivato cliccandoci sopra, da un altro messaggio in ingresso o da un particolare blocco chiamato bang.

GUI

Il terzo blocco dell’esempio precedente fa parte dei blocchi GUI (graphical user interface); tra questi sono inclusi i blocchi numerici, blocchi contenenti simboli, controlli scorrevoli e pulsanti. Mentre gli oggetti rimangono immutati durante l’esecuzione di una patch, i blocchi GUI aggiornano il loro stato in base al valore che contengono.

Commenti

I commenti sono costituiti da semplice testo e non sono contenuti all’interno di nessun rettangolo. Nella figura precedente i testi alla destra dei blocchi sono commenti.

Una patch può essere in modalità edit oppure in modalità running: nel primo caso la patch non è in esecuzione ed è permessa la creazione o modifica dei blocchi e dei collegamenti; nel secondo caso la patch è in esecuzione, è possibile ancora modificare i collegamenti, mentre la modifica dei blocchi GUI ha l’effetto di variare i parametri di controllo della patch.

L’incapsulamento in Pure Data

Come avviene con i linguaggi di programmazione quali C, C++ e Java, con Pure Data è possibile scrivere del codice che può poi essere riutilizzato in qualsiasi momento; uno o più oggetti infatti possono essere costituiti da subpatch, ovvero delle patch separate che vengono incapsulate all’interno dell’oggetto. Si possono distinguere due tipi di incapsulamento:

• one–off subpatch – se l’oggetto viene chiamato pd o pd my-name, viene creata una subpatch il cui contenuto viene salvato come parte della patch genitore che può essere riutilizzata e modificata più volte all’interno di quest’ultima;

• astrazione – se l’oggetto ha il nome di una patch già presente come file (omettendo l’estensione .pd), PD caricherà il contenuto del file all’interno della subpatch; in tal caso un cambiamento alla patch si propaga a tutte le chiamate alla sua astrazione.

Per definire il numero di inlet e outlet che deve possedere l’oggetto contenente la subpatch è sufficiente utilizzare all’interno di quest’ultima i blocchi inlet e outlet (oppure inlet~ e outlet~ per i collegamenti di segnale).

Gestione dei segnali audio

In Pure Data i segnali audio vengono memorizzati come numeri in virgola mobile a 32 bit; a seconda dell’hardware utilizzato però l’output viene limitato a 16 o 24 bit. L’input è sempre compreso tra i valori 1 e -1, mentre l’output viene tagliato al fine di restare compreso tra questi due limiti. La frequenza di campionamento di default è 44100 Hz (modificabile da riga di comando o nel menù audio setup).

Le computazioni audio vengono eseguite dai blocchi tilde, cioè quelli che, per convenzione, hanno il nome seguito da una tilde, come sc~; essi comunicano attraverso connessioni di segnale. All’avvio della computazione, o quando vengono cambiati i collegamenti, gli oggetti tilde vengono ordinati secondo un ordine di esecuzione lineare; tale lista viene poi eseguita in blocchi di 64 campioni ciascuno (a 44.1 KHz significa che l’intera rete di blocchi audio viene eseguita una volta ogni 1.45 millisecondi). Le connessioni nella rete audio devono essere acicliche; la presenza di eventuali cicli viene rilevata al momento del riordino dei blocchi. Ogni subpatch può avere dei collegamenti di segnale in entrata e in uscita tramite i blocchi “inlet\(\sim\)” e “outlet\(\sim\)”.

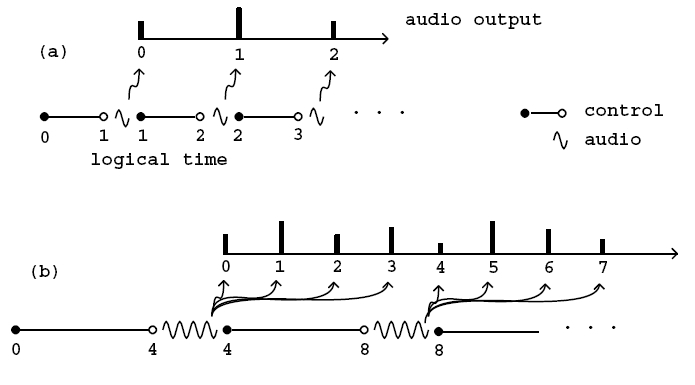
La computazione dei segnali non avviene in real time, ma in logical time: quest’ultimo è definito come l’istante del successivo campione audio che verrà elaborato, ed è sempre precedente al real time, definito come l’istante in cui il campione arriva all’output. Tutto questo serve a far sì che la computazione audio sia indipendente dal tempo effettivo di esecuzione del processore, il quale può variare per molte ragioni. Si può dedurre che una computazione audio, se eseguita nel modo corretto, è deterministica: due esecuzioni dello stesso calcolo, una in tempo reale e l’altra no, devono dare lo stesso risultato. In figura si vede come la computazione dell’audio viene svolta rispetto all’elaborazione dei segnali di controllo: i campioni audio vengono calcolati a scadenze regolari, ma prima di ogni scadenza devono essere effettuati tutti i calcoli di controllo che possono influenzare il campione audio in quella scadenza. Se \(N\) è il numero di campioni in un blocco, la prima computazione audio riguarda i campioni da \(0\) a \(N-1\), i quali vengono inviati in output tutti insieme all’istante \(N\) (logical time); prima di questo istante vengono effettuate tutte le elaborazioni di controllo per gli \(N\) campioni.

Conversione tra segnali audio e segnali di controllo

La conversione da segnale di controllo a segnale audio è possibile utilizzando l’oggetto sig~. Per quanto riguarda la conversione inversa (da segnale a controllo) deve essere specificato l’istante nel quale il segnale viene campionato; questo può essere gestito tramite l’oggetto snapshot~ che campiona il segnale ogni volta che riceve in input un bang. Gli oggetti +~, -~, *~, /~, osc~ e phasor~ possono essere configurati per accettare entrambi i tipi di segnale.

Selettori e blocchi

Gli oggetti switch~ e block~ sono utilizzati per attivare o disattivare parti della computazione audio e per controllare la dimensione dei blocchi di calcolo; deve essere presente uno solo dei due oggetti per ogni finestra della patch e il suo effetto verrà esteso a tutte le subpatch. Entrambi accettano due argomenti per la loro costruzione: il primo è la dimensione del blocco e il secondo un fattore di sovrapposizione.

L’oggetto switch~ può essere usato per ridurre il carico computazionale scegliendo, ad esempio, uno tra diversi algoritmi di sintesi da utilizzare: per farlo è sufficiente che ogni algoritmo sia implementato in una subpatch diversa.

Connessioni esterne

I segnali possono essere inviati non solo tra blocchi di una stessa finestra, ma anche tra finestre diverse oppure possono essere dati in input all’algoritmo che li ha generati in una configurazione in retroazione. Questo può essere implementato attraverso tre coppie di oggetti:

throw\(\sim\)/catch\(\sim\) –

throw~ accumula dati in un bus, mentre catch~ legge i dati accumulati e riazzera il bus per il ciclo successivo;

send\(\sim\)/receive\(\sim\) –

send~ salva un segnale che può essere ricevuto più volte da un blocco receive~, il quale però può leggere un solo send~ alla volta;

delread\(\sim\)/delwrite\(\sim\) –

se viene inviato un segnale ad un punto precedente nella rete audio, esso viene ricevuto solo al ciclo successivo, con un ritardo quindi di 1.45 millisecondi (con le impostazioni di default). Gli oggetti delread~ e delwrite~ permettono di ridurre al minimo tale ritardo.

Scheduling

Lo scheduler di Pure Data cerca di mantenere un certo vantaggio sul calcolo in modo da poter assorbire eventuali forti incrementi nel carico computazionale; tale comportamento può essere impostato tramite le flag “audiobuffer” o “frags”.

Se durante l’elaborazione dell’audio si accumulano dei ritardi, possono verificarsi delle interruzioni nei flussi di input e output; tuttavia lo streaming su disco non viene influenzato.

Le operazioni di PD sono deterministiche, nel senso che le computazioni vengono eseguite nel momento in cui vengono schedulate senza subire cambiamenti di ordine in real–time. Se un’operazione viene attivata da un evento esterno, viene associata ad un tempo; questo serve a garantire che le esecuzioni siano consistenti con le scadenze temporali imposte dallo scheduler (il tempo non deve mai decrescere).

Scrivere external per Pure Data

Con il termine external si indica un oggetto che non è compreso in Pure Data ma che può essere caricato dinamicamente durante l’esecuzione di PD; si differenziano dagli internal in quanto questi ultimi sono le primitive già incluse in PD. Una volta che un external viene caricato in memoria, non è più distinguibile dagli internal. Una libreria è una collezione di external compilati all’interno di un unico file binario; il nome di una libreria varia a seconda del sistema operativo per la quale viene implementata: ad esempio, se viene creata la libreria my_lib, essa dovrà essere chiamata my_lib.pd_linux nei sistemi Linux, my_lib.pd_irix e my_lib.dll nei sistemi Win32. Una libreria elementare include esattamente un external avente lo stesso nome della libreria.

A differenza degli external, una libreria può essere importata in due modi:

• tramite opzione da riga di comando: -lib my_lib (così la libreria e tutti gli external in essa contenuti vengono caricati all’avvio di PD);

• creando un oggetto my_lib (consigliabile quando la libreria contiene un solo oggetto con il nome della libreria stessa).

In entrambi i casi PD prima controlla se una libreria my_lib è già stata caricata; se così non è, viene cercato il file corrispondente e, se trovato, tutti gli external inclusi vengono caricati.

Pure Data è scritto in C, quindi anche gli external vanno scritti in questo linguaggio di programmazione; il codice per un semplice external che stampa il messaggio “hello world!” è riportato di seguito (Zmölnig, J. M., n.d.):

    #include "m_pd.h"

    static t_class *helloworld_class;

    typedef struct _helloworld {
    t_object x_obj;
    } t_helloworld;

    void helloworld_bang(t_helloworld *x)
    {
        post("Hello world !!");
    }

    void *helloworld_new(void)
    {
        t_helloworld *x = (t_helloworld *)pd_new(helloworld_class);
        return (void *)x;
    }

    void helloworld_setup(void)
    {
        helloworld_class = class_new(gensym("helloworld"),
                                                (t_newmethod)helloworld_new,
                                                0, sizeof(t_helloworld),
                                                CLASS_DEFAULT, 0);
        class_addbang(helloworld_class, helloworld_bang);
    }

Inizialmente viene definita la nuova classe (qui il termine “classe” viene usato con un significato diverso da quello usuale della programmazione ad oggetti), dove hello_worldclass è un puntatore alla nuova classe e la struttura t_helloworld costituisce il dataspace della classe; la variabile t_object è assolutamente necessaria e serve a memorizzare le proprietà dell’oggetto, come la sua rappresentazione grafica e le informazioni su inlet e outlet.

Vengono poi definite le funzioni (methods) per manipolare i dati; quando l’istanza della classe riceve un dato, viene richiamato un metodo; ogni metodo è associato ad un inlet. La funzione implementata viene eseguita solo quando un nuovo dato arriva a tale inlet.

Al caricamento della libreria, PD richiama la funzione helloworld_setup(): tale funzione dichiara la nuova classe e le sue proprietà. L’istruzione class_new crea una nuova classe e ritorna un puntatore ad essa: il primo argomento è il nome simbolico della classe; il secondo e il terzo definiscono il costruttore e il distruttore; il quarto definisce la dimensione della struttura dati; il quinto determina l’aspetto grafico dell’oggetto; i rimanenti sono gli argomenti dell’oggetto. L’istruzione successiva serve per aggiungere i metodi alla classe (il primo argomento è la classe, il secondo è il metodo).

L’inizializzazione dell’oggetto avviene tramite la funzione helloworld_new(), i cui argomenti dipendono dalla definizione data con class_new.

Librerie utili per Pure Data

GEM

GEM (acronimo per Graphical Environment for Multimedia, http://gem.iem.at) è una collezione di external che permettono di integrare elaborazioni grafiche OpenGL in una patch; sono disponibili diversi tipi di forme geometriche, di luci e di texture; è possibile implementare il movimento della visuale e processare l’immagine.

Le elaborazioni della parte audio e della grafica vengono svolte contemporaneamente: in tal modo si può creare un vero e proprio scenario virtuale semplicemente utilizzando una rete di blocchi creati e gestiti come i blocchi nativi di PD.

Flext

Si è visto che Pure Data è un software scritto in C, e gli external devono essere scritti in tale linguaggio; l’utente però potrebbe avere la necessità di usare le meno complesse strutture del C++, nonché il pieno supporto alla programmazione ad oggetti che questo offre. Per soddisfare questa esigenza nasce flext (http://grrrr.org/ext/flext/), una libreria per lo sviluppo di external in C++. Con flext è possibile creare librerie di external che possono essere compilate per Pure Data, per Max/MSP e per differenti piattaforme (Windows, Linux, OSX) e compilatori.

Un semplice esempio di external basato su flext è il seguente.

    // inclusione del header file
    #include <flext.h>

    // controllo sulla versione
    #if !defined(FLEXT_VERSION) || (FLEXT_VERSION < 400)
    #error You need at least flext version 0.4.0
    #endif

    // definizione della classe
    // Attenzione: il nome della classe deve essere lo stesso
    // nome dell'oggetto (senza l'eventuale ~)
    class simple1:

    public flext_base
    {
        FLEXT_HEADER(simple1,flext_base)

        public:
        // costruttore
        simple1()
        {
            // definizione degli inlets:
            // il primo deve essere sempre di tipo anything
            // (oppure signal per gli oggetti dsp)
            AddInAnything(); 
    
            // definizione degli outlets:
            AddOutFloat(); // aggiunta di un outlet float (indice 0)
    
            // registrazione dei metodi:
            // registra il metodo "m_float" per l'inlet 0
            FLEXT_ADDMETHOD(0,m_float); 
        }
    
        protected:
        // definizione del metodo
        void m_float(float input)
        {
            float result;
            if(input == 0) {
            post("%s - zero can't be inverted!",thisName());
            result = 0;
            }
            else
                result = 1/input;
                
            // manda il valore in output all'outlet
            ToOutFloat(0,result); // (0 è l'indice dell'outlet)
        }

        private:
        // callback per il metodo "m_float"
        FLEXT_CALLBACK_1(m_float,float) 
    };

    // creazione della classe
    FLEXT_NEW("simple1",simple1)

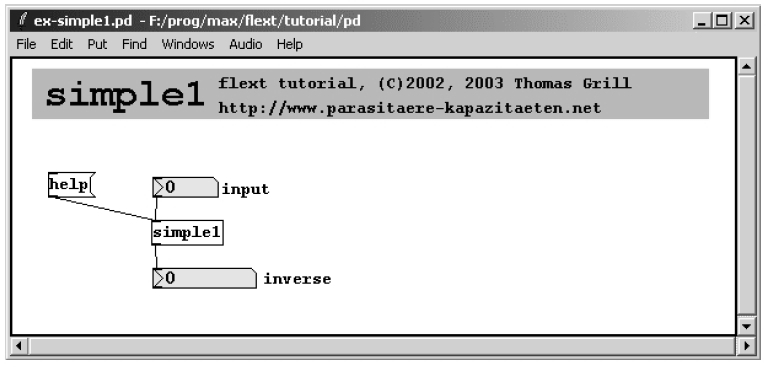
Come si può notare, è stata utilizzata la programmazione ad oggetti, a partire dalla creazione di una classe derivata dalla classe base flext_base, la quale contiene tutte le funzioni essenziali. Il costruttore viene richiamato nel momento in cui l’oggetto è incluso nella patch; più precisamente è chiamato quando si crea un’istanza della classe, contiene tutte le inizializzazioni necessarie e ha lo stesso nome della classe. Tra le inizializzazioni devono essere presenti le dichiarazioni di inlet e outlet e le associazioni tra metodi e rispettivi inlet.

Un callback wrapper è necessario per stabilire un collegamento con PD per ogni metodo che deve essere lanciato ogni volta che un dato viene ricevuto: ciò avviene tramite l’istruzione FLEXT_CALLBACK_1(m_float, float). Con l’ultimo comando si informa il sistema riguardo al nome della classe e ai suoi argomenti di creazione.

Implementazione della patch generatrice di rumore frattale

Nella realizzazione della patch per Pure Data che implementa l’algoritmo di generazione di rumore frattale, per convenienze implementative, i filtri sono stati riscritti come cascata di biquadri: perciò la cascata è formata da \(N/2\) filtri del secondo ordine, ognuno con le seguenti funzioni di trasferimento:

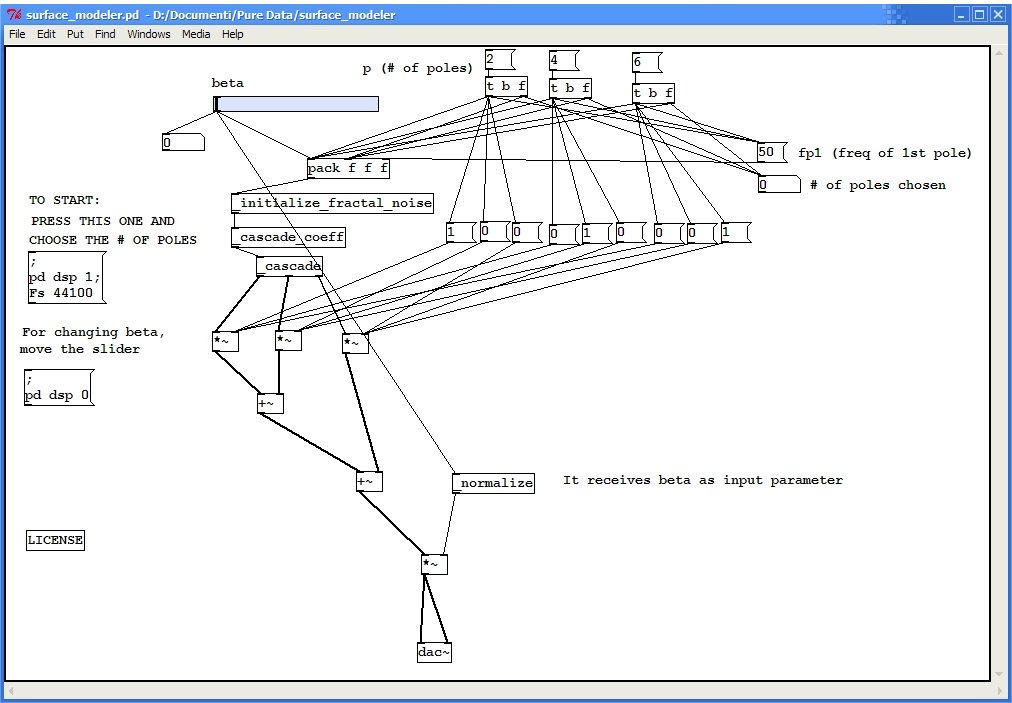
Il parametro di controllo più importante impostabile dall’utente è \(\beta\), che definisce lo spettro \(1/f^{\beta}\); deve essere impostato anche il numero di poli della cascata di filtri assieme alla frequenza del primo polo: con questi parametri viene controllata l’accuratezza dell’approssimazione \(1/f^{\beta}\).

Nella figura precedente è riportata la patch surface_modeler che implementa la generazione di rumore frattale. Per avviare la computazione è sufficiente cliccare sul blocco (in modalità running):

subito dopo si seleziona il numero di poli desiderato (due, quattro o sei). Il controllo sulla patch avviene variando il parametro \(\beta\) tramite lo slider:

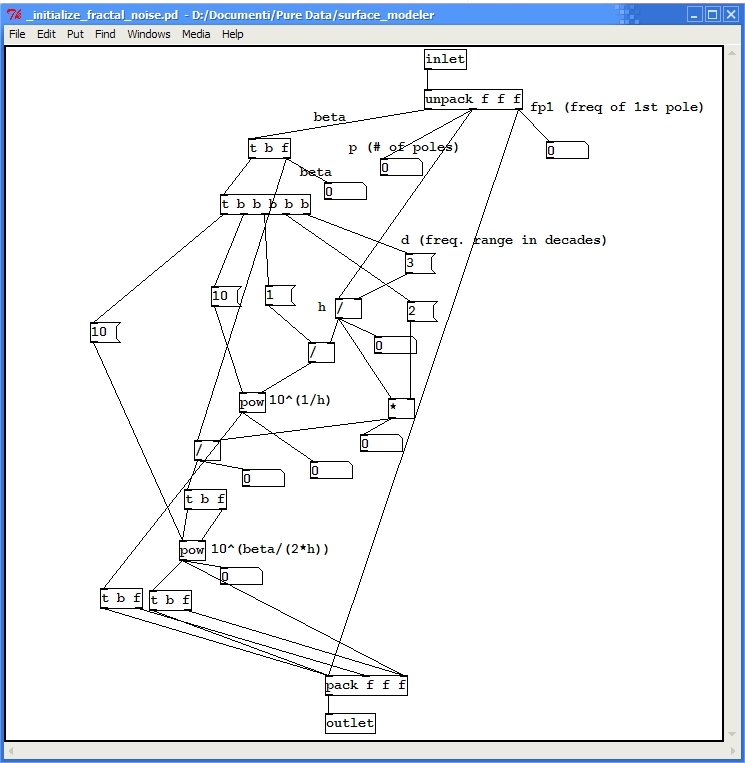
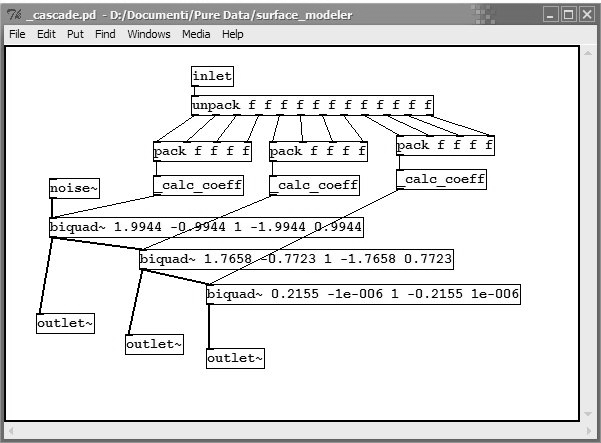
Il modulo _cascade invece è una subpatch nella quale viene implementata una cascata di tre filtri; ogni oggetto biquad~ è un filtro biquadro a due poli e due zeri; ognuno di questi filtri calcola le seguenti equazioni differenziali:

I valori \(fb1, fb2, ff1, ff2, ff3\) vengono dati, in quest’ordine, come argomenti di creazione dell’oggetto.

Implementazione della patch generatrice di rumore di sfregamento

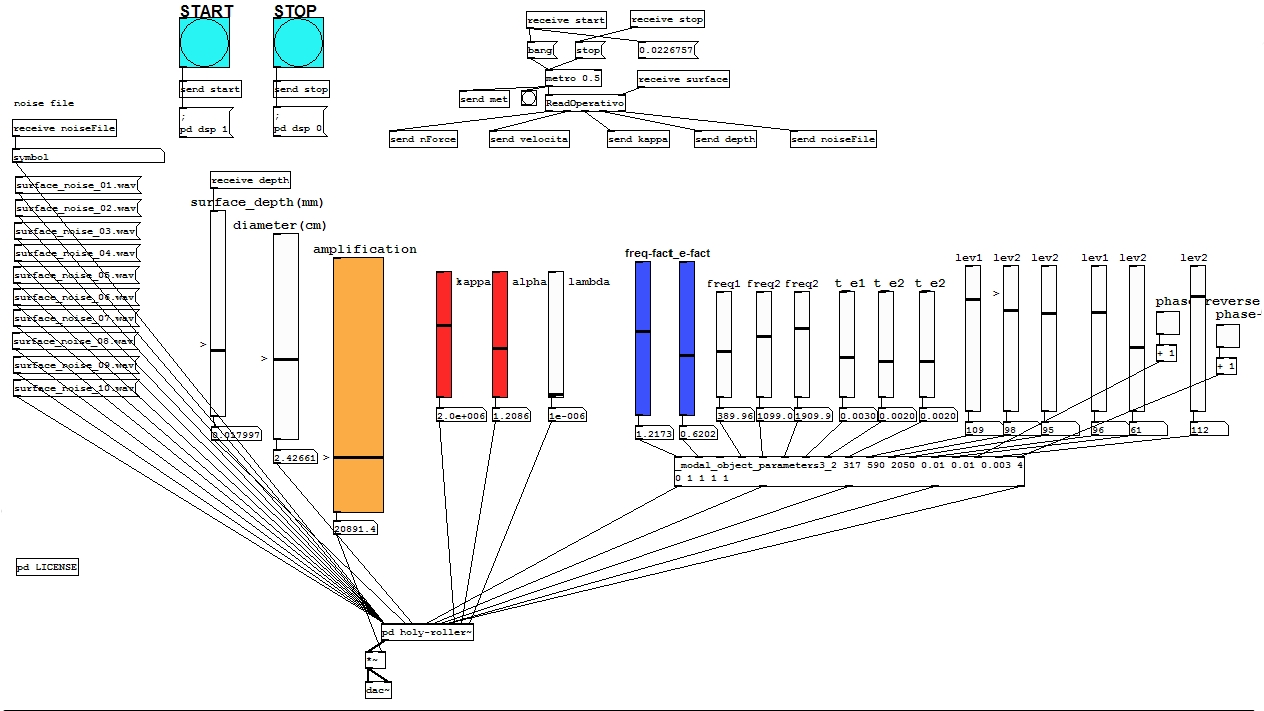
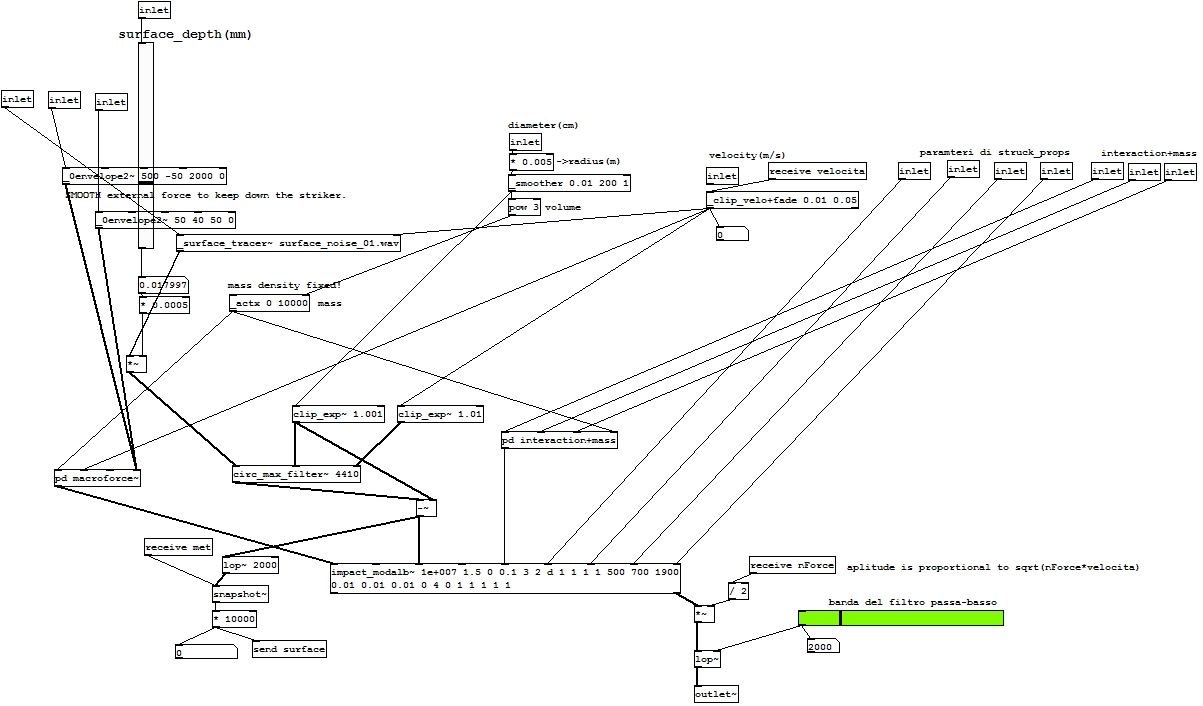
Come abbiamo visto è stato sviluppato un modello che descrive il suono per un corpo che rotola sopra una superficie. Se il corpo, invece di rotolare, striscia sulla superficie, provoca sempre la generazione di micro–contatti, che tuttavia avvengono con modalità diverse rispetto al rotolamento.

Una prima distinzione si ha nella velocità con cui avviene il contatto: se per il modello di rotolamento deve essere presa in considerazione la velocità angolare dell’oggetto che rotola (che nel caso di una sfera si calcola come \(\omega = v/r\), con \(r\) raggio della sfera), per un corpo che striscia si deve considerare la velocità tangenziale, cioè la velocità lungo il piano sul quale giace la superficie. In secondo luogo il suono di un moto di rotolamento è spesso caratterizzato da irregolarità periodiche dovute alle caratteristiche particolari del corpo che rotola. Se questo non è perfettamente sferico e perfettamente liscio, i micro–contatti non saranno tutti uguali ma varieranno; in particolare per un corpo che rotola i micro–contatti si presentano con le stesse caratteristiche a scadenze periodiche (variabili con la velocità di movimento), e ciò si riflette nel suono prodotto, il quale sarà caratterizzato da variazioni periodiche. Per un corpo che striscia invece le irregolarità della sua superficie non comportano caratteristiche periodiche nel suono. Tutto ciò è valido se la dimensione del corpo è sufficientemente grande rispetto alla tessitura della superficie sulla quale si muove.

La patch che implementa la generazione di rumore di sfregamento è stata quindi elaborata a partire dalla patch che implementa il modello di rotolamento.

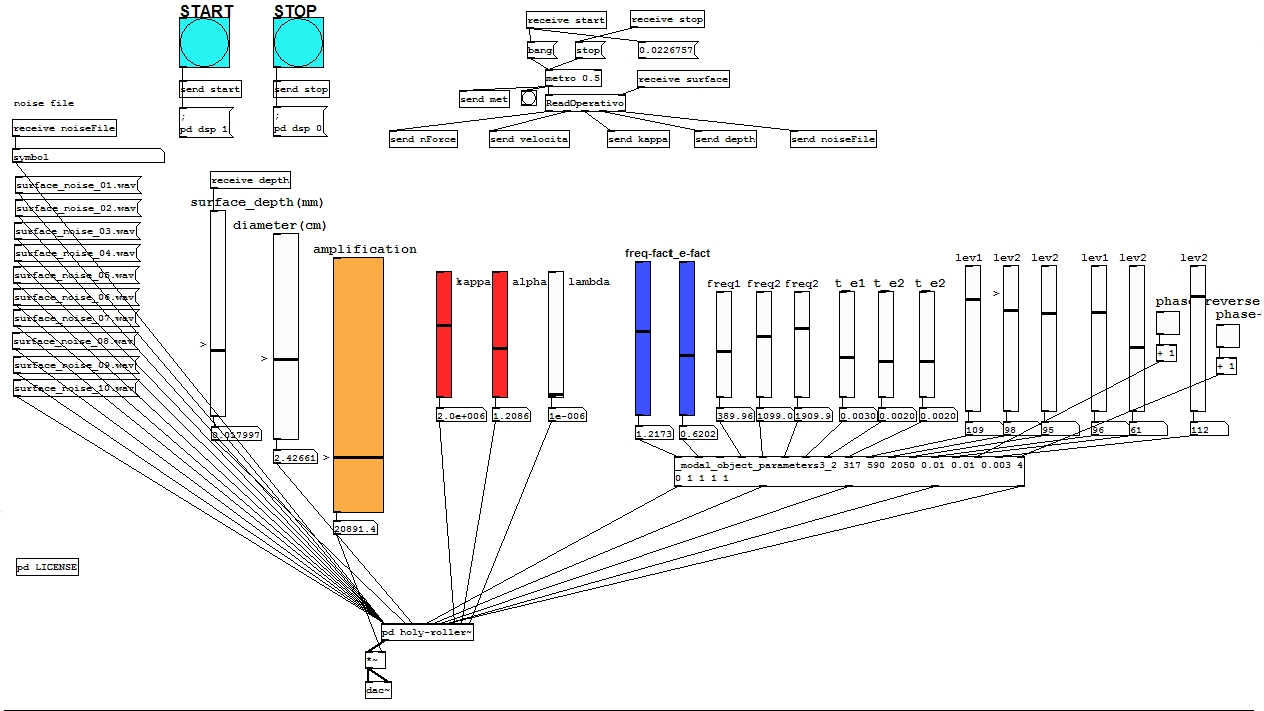
holy-roller\(\sim\)

Il cuore della computazione viene svolto dalla subpatch holy_roller~; l’oggetto holy_roller~ possiede 13 inlet:

• inlet 0 – accetta un oggetto di tipo messaggio contente il nome di un file .wav; tale file è stato precedentemente ottenuto registrando per circa 10 secondi l’output della patch generatrice di rumore frattale (e pertanto contiene a sua volta un rumore frattale);

• inlet 1 e 2 – non utilizzati in questa implementazione; accettano entrambi un segnale utilizzato poi come forza aggiuntiva da applicare all’oggetto rotolante;

• inlet 3 – accetta un numero in virgola mobile proporzionale all’amplificazione in ampiezza che deve subire il rumore frattale;

• inlet 4 – assumendo che l’oggetto che si muove sulla superficie sia una sfera, questo inlet riceve un numero in virgola mobile corrispondente al diametro della sfera in centimetri; sarà poi utilizzato per calcolarne la massa;

• inlet 5 – riceve un numero in virgola mobile indicante la velocità (in \(m/s\)) dell’oggetto che si muove;

• inlet 6, 7, 8 e 9 – ricevono tutti dei segnali di controllo per l’impostazione delle frequenze e i tempi di decadimento degli oggetti modali usati nel modello di impatto (il tempo di decadimento è definito come il tempo richiesto affinché l’ampiezza decresca di un fattore \(1/e\) rispetto al suo valore iniziale);

• inlet 10 – riceve un numero in virgola mobile (\(k\)) proporzionale alla rigidità dell’oggetto;

• inlet 11 e 12 – ricevono due numeri in virgola mobile (\(\alpha\) e \(\lambda\)) utilizzati nel modulo impact_modalb~ per il calcolo della forza di impatto.

Elaborazione di diametro e velocità

Il valore del diametro viene elaborato da alcuni blocchi allo scopo di calcolare dei valori indicanti il volume e la massa dell’oggetto rotolante.

Il modulo _smoother ha lo scopo di trasformare una variazione istantanea del valore del diametro secondo una rampa lineare della durata di un millisecondo.

Il valore di velocità invece viene inviato in input all’oggetto _clip_velo+fade; tale oggetto invia al primo outlet il valore di input se questo è maggiore del valore dato come primo argomento di costruzione (che nell’implementazione è \(0.01\)), altrimenti viene inviato quest’ultimo. Il ruolo di questo outlet è impedire che alla patch successiva clip_exp~ venga inviato costantemente un segnale di controllo nullo; se ciò si verificasse infatti si creerebbe un ciclo infinito che porterebbe ad un funzionamento non corretto della patch. Al secondo outlet viene inviato il valore ricevuto all’inlet opportunamente scalato nell’intervallo delimitato dai due argomenti.

clip_exp\(\sim\)

I valori di raggio (in metri) e di velocità (in metri al secondo) vengono inviati ai due oggetti clip_exp~, la cui funzione è quella di limitare la variazione logaritmica dei segnali in input. Più precisamente, in ognuno dei due oggetti viene per prima cosa calcolato il rapporto tra due campioni in input a distanza di un millisecondo l’uno dall’altro; se tale rapporto è maggiore di maxfact o minore di minfact (calcolati a partire dal parametro di costruzione), il valore del campione corrente viene limitato e inviato all’outlet. Se il rapporto è minore del valore predeterminato, il campione viene inviato in output invariato. Il codice seguente mostra come questo algoritmo sia implementato (per ragioni di efficienza) in C.

    static t_int *clip_exp_tilde_perform(t_int *w)
    {
      t_float *in = (t_float *)(w[1]);
      t_float *out = (t_float *)(w[2]);
    
    t_clip_exp_tilde_ctl *c = (t_clip_exp_tilde_ctl *)(w[3]);
    t_int buffersize = (t_int)(w[4]);

    t_float input, ratio;

        // esamina tutto il buffer
    while (buffersize--)
        {
        input = *in++;

            // se last è diverso da zero
        if (c->last != 0.)
            {
                // se ratio è compreso tra maxfact e minfact
                // in ouput viene mandato input
                // altrimenti l'output è impostato a maxfact o minfact
            ratio = input / c->last;
        
            if (ratio > c->maxfact)
                c->last *= c->maxfact;
            
            else if (ratio < c->minfact)
                c->last *= c->minfact;
            
            else
                c->last = input;
            }

      *out++ = c->last;
    }

    return (w+5);
    }

I valori maxfact e minfact vengono calcolati nel seguente modo:

    static void set_expmax(t_clip_exp_tilde *x, t_floatarg expmax)
    {
      t_clip_exp_tilde_ctl *c = x->x_ctl;

        // se l'argomento del modulo è < 1
        // pongo maxfact e minfact = 1
      if (expmax <= 1.)
    {
        c->maxfact = c->minfact = 1.;
      post("clip_exp: expmax <= 1?! Is set to 1.");
    }
    // atrimenti:
    // maxfact = epmax^(1000/samprate)
    else
    {
        c->maxfact = pow(expmax, 1000. / x->samprate);
      c->minfact = 1. / c->maxfact;
    }
    }

circ_max_filter\(\sim\)

Gli outlet dei due moduli clip_exp~ sono collegati al secondo e terzo inlet dell’oggetto circ_max_filter~:

la sua funzione è quella di tracciare il profilo della superficie sulla quale l’oggetto rotola e calcolare i punti di contatto tra i due. Nel primo inlet entra il controllo di segnale ottenuto dalla moltiplicazione del rumore frattale per il fattore di amplificazione surface_depth. Il ciclo principale svolto dal modulo è il seguente:

static t_int *circ_max_filter_perform(t_int *w)
{
    t_float *in1 = (t_float *)(w[1]);
    t_float *in2 = (t_float *)(w[2]);
    t_float *in3 = (t_float *)(w[3]);
    t_float *out = (t_float *)(w[4]);

    t_circ_max_filter_ctl *c = (t_circ_max_filter_ctl *)(w[5]);
    t_float *p_samprate = (t_float *)(w[6]);
    t_int buffersize = (t_int)(w[7]);

    t_float input, radius, velocity;
    t_int range;

    while (buffersize--)
    {
        input = *in1++;
        radius = *in2++;
        velocity = *in3++;

        inc_bottom_ivalue1_circ_buff_1float2int(c->p_peaks, -1);

        while ((range = bottom_ivalue1_circ_buff_1float2int(c->p_peaks))
                < bottom_ivalue2_circ_buff_1float2int(c->p_peaks))
        {
            delete_bottom_circ_buff_1float2int(c->p_peaks);
            inc_bottom_ivalue1_circ_buff_1float2int(c->p_peaks, range);
        }
    
        *out++ = up_circle(velocity * range / *p_samprate, radius)
                + bottom_fvalue_circ_buff_1float2int(c->p_peaks);

        to_buffer(c->p_peaks, *p_samprate, input, radius, velocity, 1);
    }

    return (w+8);
}

In particolare si può notare come l’istruzione

    *out++ = up_circle(velocity * range / *p_samprate, radius)
            + bottom_fvalue_circ_buff_1float2int(c->p_peaks);

calcola i punti di contatto svolgendo la computazione della funzione \(f_x(q)\).

La funzione up_circle richiede due argomenti; dopo aver calcolato i quadrati di questi, ritorna la radice quadrata della differenza dei due:

    static INLINE t_float up_circle(t_float x, t_float radius)
    {
        t_float x_2 = x*x, radius_2 = radius*radius;

        if (x_2 >= radius_2)
        {
          return(0.);
        }
        else
            return(sqrt(radius_2 - x_2));
    }

La funzione to_buffer si occupa di aggiornare il profilo della superficie in base al segnale ricevuto al primo inlet.

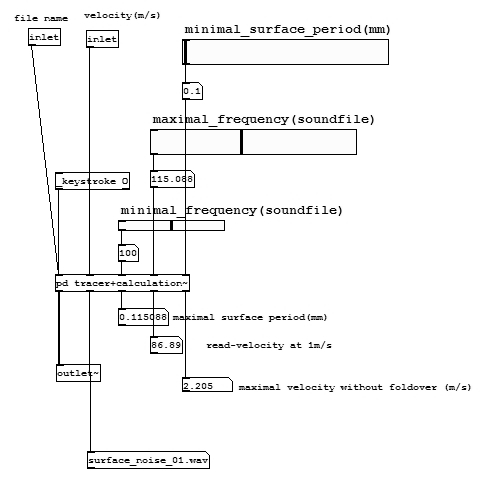
_surface_tracer\(\sim\)

Il file con estensione .wav contenente il rumore frattale viene letto dalla subpatch _surface_tracer~. Questa subpatch, assieme alle subpatch in essa contenute quali pd tracer+calculation~, soundfiler_tracer~ e table_tracer~, legge il file audio e lo scrive in un array; successivamente, per inviare i campioni in output, esegue una ricerca di tipo table look–up con frequenza dipendente dalla velocità di movimento dell’oggetto sulla superficie.

impact_modalb\(\sim\)

Le successive elaborazioni dei segnali finora calcolati sono svolte dal modulo impact_modalb~, un oggetto che implementa il modello descritto in (Avanzini, F., Rath, M., & Rocchesso, D., 2003) per i suoni di impatto.

In questa implementazione vengono utilizzati due modi e tre punti di interazione.

I parametri della forza di contatto e della massa vengono ricevuti dalla subpatch interaction+mass e la subpatch in essa contenuta _par_to_list4; in output (secondo outlet) viene mandata una lista contenente queste informazioni. Nei quattro inlet vengono ricevuti, in ordine: \(k\), \(\alpha\), \(\lambda\) e la massa del percussore.

La subpatch _modal_object_parameters3_2, dove 3 è il numero di modi e 2 il numero di punti di interazione, raccoglie i parametri del risonatore. Nei primi tre inlet entrano i fattori moltiplicativi per frequenza, tempo di decadimento e guadagno; ai successivi tre inlet sono collegati i controlli delle frequenze di tutti i modi, poi i tempi di decadimento di tutti i modi. Gli ultimi inlet ricevono i livelli di ciascun modo per ogni punto di interazione con l’eventuale possibilità di invertire la fase (phase–reverse). In uscita sono presenti cinque outlet: il primo per la lista dei fattori, il secondo per la lista delle frequenze, il terzo per la lista dei tempi di decadimento e un outlet per ogni punto di interazione con l’indice del punto di interazione seguito dalla lista dei livelli (con l’eventuale fattore di phase reverse). Infine l’oggetto _modal_object_parameters3_2 deve essere inizializzato con la seguente lista di argomenti: lista dei valori delle frequenze, lista dei valori dei tempi di decadimento, valori dei punti di interazione e del phase–reverse; un valore 1 per il livello corrisponde ad una impostazione del relativo slider a 100, dato che quest’ultimo viene convertito in dB RMS.

L’oggetto impact_modalb~ possiede i seguenti argomenti di costruzione:

• valori di default di \(k\), \(\alpha\), \(\lambda\) e massa del percussore;

• numero di modi e numero di punti di interazione;

• maschera dei punti di interazione;

• valori di default dei tre fattori di guadagno;

• valori di default delle frequenze;

• valori di default dei tempi di decadimento;

• per ogni punto di interazione il suo indice (partendo da 0) seguito dai valori dei livelli.

Dipendenza dell’ampiezza del suono dalla forza normale

Secondo studi svolti da Van Den Doel, Kry e Pai [@art:vandendoel], nei contatti che avvengono tra due corpi e che coinvolgono forze di frizione, queste ultime sono calcolabili come: \(F_{frizione} = \mu F_{normale}\) e il volume del suono prodotto da ogni contatto è proporzionale a \(\sqrt{v \cdot F_{normale}}\), dove \(v\) è la velocità alla quale avviene il contatto; in questo calcolo si assume che l’energia acustica sia proporzionale alla perdita di capacità da parte della superficie di opporre una resistenza (di frizione) al moto. Nella subpatch holy_roller~ tale caratteristica è implementata tramite gli oggetti in figura:

Riferimenti

1. Avanzini, F., Rath, M., & Rocchesso, D. (2003). Low-level sound models: resonators, interactions, surface textures. The Sounding Object, 119–148.
2. Hastings, H. M., & Sugihara, G. (1993). Fractals: A User’s Guide for the Natural Sciences. Oxford University Press.
3. Resnick, S. (1992). Adventures in Stochastic Processes. Birkhäuser Boston.
4. Wornell, G. W. (1998). The Digital Signal Processing Handbook. CRC Press and IEEE Press.
5. Pentland, A. P. (1988). Fractal-Based Description Of Surfaces. Natural Computation, 279–298.
6. Saletti, R. (Novembre 1986). A comparison between two methods to generate 1/f^γnoise. Proc. IEEE, 74, 1595–1596.
7. Corsini, G., & Saletti, R. (Dicembre 1988). A 1/f^γpower spectrum noise sequence generator. IEEE Trans. on Instrumentation and Measurement, 37(4), 615–619.
8. Mitra, S. K. (1998). Digital Signal Processing: A Computer Based Approach. McGraw-Hill.
9. Zmölnig, J. M. HOWTO write an external for puredata. Institut for electronic music and acoustics.